Get in Touch With Us
Submitting the form below will ensure a prompt response from us.
In machine learning, Lasso (Least Absolute Shrinkage and Selection Operator) is a powerful regularization technique that helps prevent overfitting and improve model interpretability. It is especially useful in regression problems where the model has too many features.
This article explores what Lasso Machine Learning is, how it works, its mathematical formulation, and how to implement it using Python.
What is Lasso Regression?
Lasso regression is a type of linear regression that adds an L1 regularization term to the cost function. This penalty term shrinks some coefficient values toward zero, effectively performing feature selection by eliminating less important variables.
Mathematical Representation
The cost function for Lasso regression is:
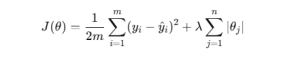
Where:
- m → number of training samples
- yi → actual output
- y^i→ predicted output
- λ → regularization strength
- θj → model coefficients
When λ\lambdaλ is large, more coefficients become zero — meaning the model uses fewer features.
Why Use Lasso in Machine Learning?
Lasso regression is widely used for several key reasons:
- Feature Selection – Automatically removes irrelevant features.
- Prevents Overfitting – Controls model complexity.
- Improves Interpretability – Simplifies the model by retaining only key variables.
- Enhances Performance – Especially effective for high-dimensional datasets.
Lasso vs Ridge Regression
| Feature | Lasso Regression | Ridge Regression |
|---|---|---|
| Regularization Type | L1 (absolute value) | L2 (squared value) |
| Feature Selection | Yes (sets some weights to zero) | No |
| Output Coefficients | Sparse | Shrunk but non-zero |
| Best Used For | High-dimensional data | Multicollinearity problems |
In many real-world applications, a hybrid of both — Elastic Net — is used to combine their benefits.
Python Example: Lasso Regression in Action
Let’s demonstrate how to use Lasso regression in Python using scikit-learn.
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
# Generating sample data
X = np.random.rand(100, 5)
y = 3*X[:,0] + 2*X[:,1] + np.random.randn(100) * 0.2
# Splitting data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Applying Lasso regression
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)
# Predictions
y_pred = lasso.predict(X_test)
print("Coefficients:", lasso.coef_)
print("Mean Squared Error:", mean_squared_error(y_test, y_pred))Output Example:
Coefficients: [2.98 1.95 0. 0. 0. ]
Mean Squared Error: 0.042Notice that Lasso automatically shrinks some coefficients to zero — meaning it has effectively selected the most important features.
Visualizing Feature Shrinkage (Optional)
import matplotlib.pyplot as plt
alphas = np.logspace(-3, 1, 50)
coefs = []
for a in alphas:
model = Lasso(alpha=a, fit_intercept=False)
model.fit(X_train, y_train)
coefs.append(model.coef_)
plt.plot(alphas, coefs)
plt.xscale('log')
plt.xlabel('Alpha')
plt.ylabel('Coefficient Magnitude')
plt.title('Lasso Coefficients Shrinking with Alpha')
plt.show()This graph illustrates how the coefficients approach zero as the regularization strength (λ) increases.
When to Use Lasso Machine Learning?
- When you have many correlated or irrelevant features.
- When model interpretability is crucial.
- When you need sparse solutions (few non-zero coefficients).
- For predictive modeling in finance, healthcare, and text analytics.
Boost Model Performance Using Lasso
Our data scientists fine-tune machine learning models using Lasso regression to eliminate noise and overfitting.
Conclusion
Lasso Machine Learning is a crucial regularization method for enhancing model simplicity and mitigating overfitting. By adding an L1 penalty, it not only enhances prediction accuracy but also performs built-in feature selection.
Whether you’re working on regression, financial modeling, or data-driven analytics, mastering Lasso can make your models leaner, more interpretable, and more efficient.













