Get in Touch With Us
Submitting the form below will ensure a prompt response from us.
Every machine learning model has one primary goal — to minimize errors and make accurate predictions. To measure how well (or poorly) a model is performing, we use something called a Cost Function in Machine Learning.
This article explores what a cost function is, how it works, common types, and how to implement it in Python.
What is a Cost Function in Machine Learning?
A Cost Function, also known as a Loss Function, measures the difference between the predicted output and the actual output of a model.
The main objective during training is to minimize this cost, so the model learns to make predictions as close as possible to the true values.
Mathematically:
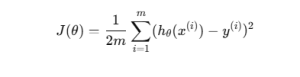
Where:
- J(θ) → Cost function
- hθ(x(i)) → Model prediction
- y(i) → Actual output
- m → Number of training samples
Why Cost Functions Are Important?
- Performance Evaluation – Quantifies how well the model fits the data.
- Optimization Guide – Helps the optimizer (like Gradient Descent) know how to adjust parameters.
- Model Comparison – Different algorithms can be compared using their cost values.
Without a cost function, it would be impossible to guide the model’s learning effectively.
Common Types of Cost Functions
Mean Squared Error (MSE) – Regression
Used in regression tasks to measure the average squared difference between predictions and actual values.
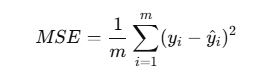
Mean Absolute Error (MAE)
Measures the average magnitude of errors without considering direction.
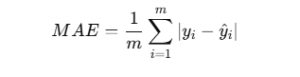
Binary Cross-Entropy – Classification
Used for binary classification models like logistic regression.
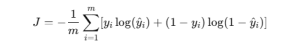
Categorical Cross-Entropy
Used for multi-class classification with Softmax output.
Python Example: Linear Regression Cost Function
Let’s compute the Mean Squared Error (MSE) for a simple regression model.
import numpy as np
# Actual and predicted values
y_true = np.array([3, 5, 7, 9])
y_pred = np.array([2.8, 5.1, 6.8, 9.2])
# Mean Squared Error
mse = np.mean((y_true - y_pred)**2)
print("Mean Squared Error:", mse)
Output:
Mean Squared Error: 0.0225
Implementing Gradient Descent to Minimize Cost
import numpy as np
# Data
X = np.array([1, 2, 3, 4])
y = np.array([3, 5, 7, 9])
# Initialize weights
w, b = 0.1, 0.1
learning_rate = 0.01
# Gradient Descent Loop
for _ in range(1000):
y_pred = w * X + b
dw = (-2/len(X)) * sum(X * (y - y_pred))
db = (-2/len(X)) * sum(y - y_pred)
w -= learning_rate * dw
b -= learning_rate * db
print("Optimized Weight:", w)
print("Optimized Bias:", b)
This simple gradient descent minimizes the cost function iteratively, adjusting weights until the error is minimal.
Visualization Example (Optional Add-on)
You can visualize how the cost decreases over iterations:
import matplotlib.pyplot as plt
iterations = np.arange(1, 101)
cost_values = np.exp(-0.05 * iterations)
plt.plot(iterations, cost_values)
plt.xlabel("Iterations")
plt.ylabel("Cost Function Value")
plt.title("Cost Function Minimization Over Time")
plt.show()This shows the cost function decreasing smoothly, which indicates successful learning.
Build Accurate Machine Learning Models
Get end-to-end ML solutions optimized with cost functions and deep learning techniques.
Conclusion
The Cost Function in Machine Learning is a fundamental concept that measures how closely predictions match reality. It plays a central role in optimization, guiding algorithms like Gradient Descent to improve model accuracy.
Whether you’re training a regression, classification, or deep learning model, understanding and tuning the cost function is essential for building models that truly learn from data.













